Options
All
  • Public
  • Public/Protected
  • All
Menu

Class AndersonianRemote

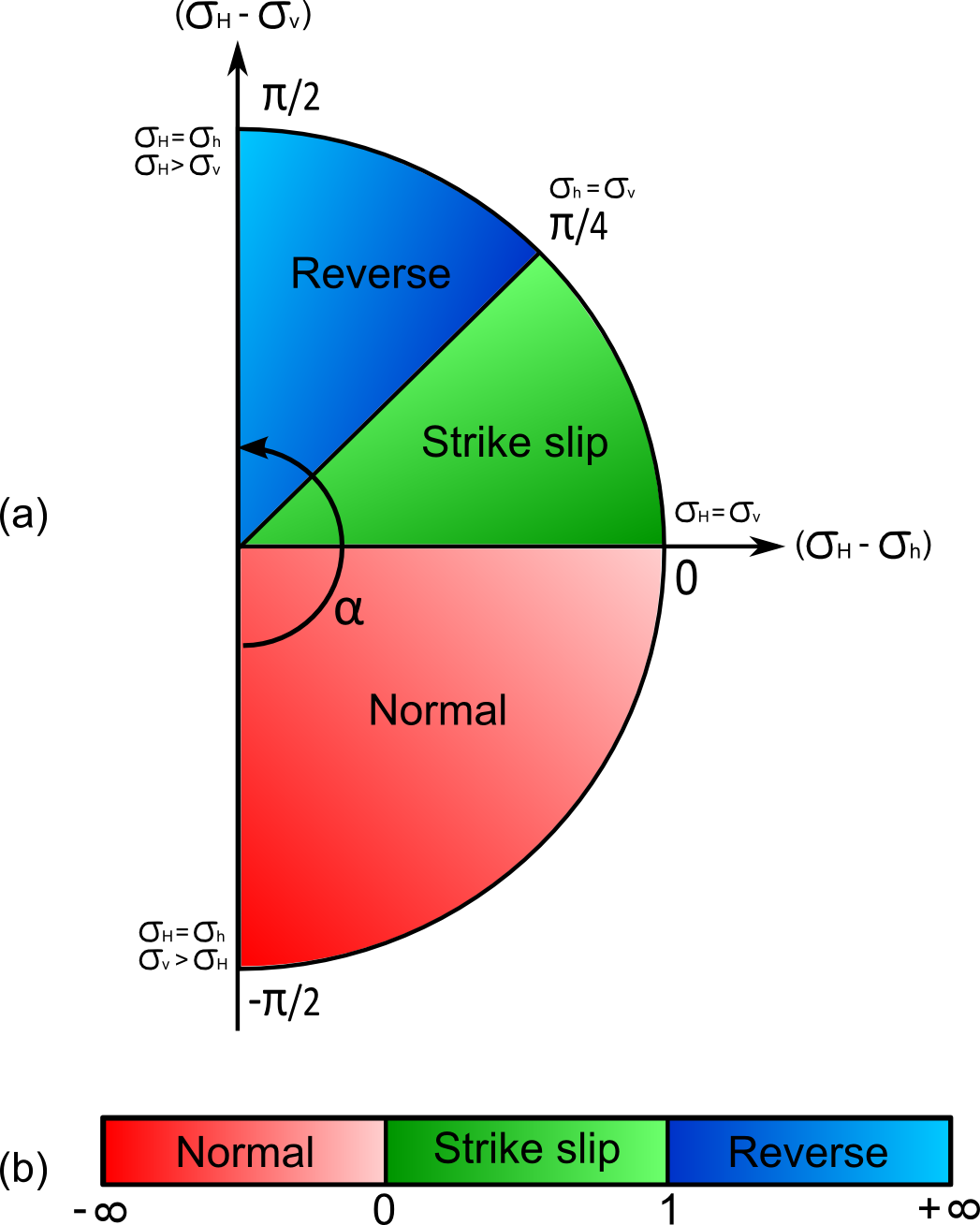
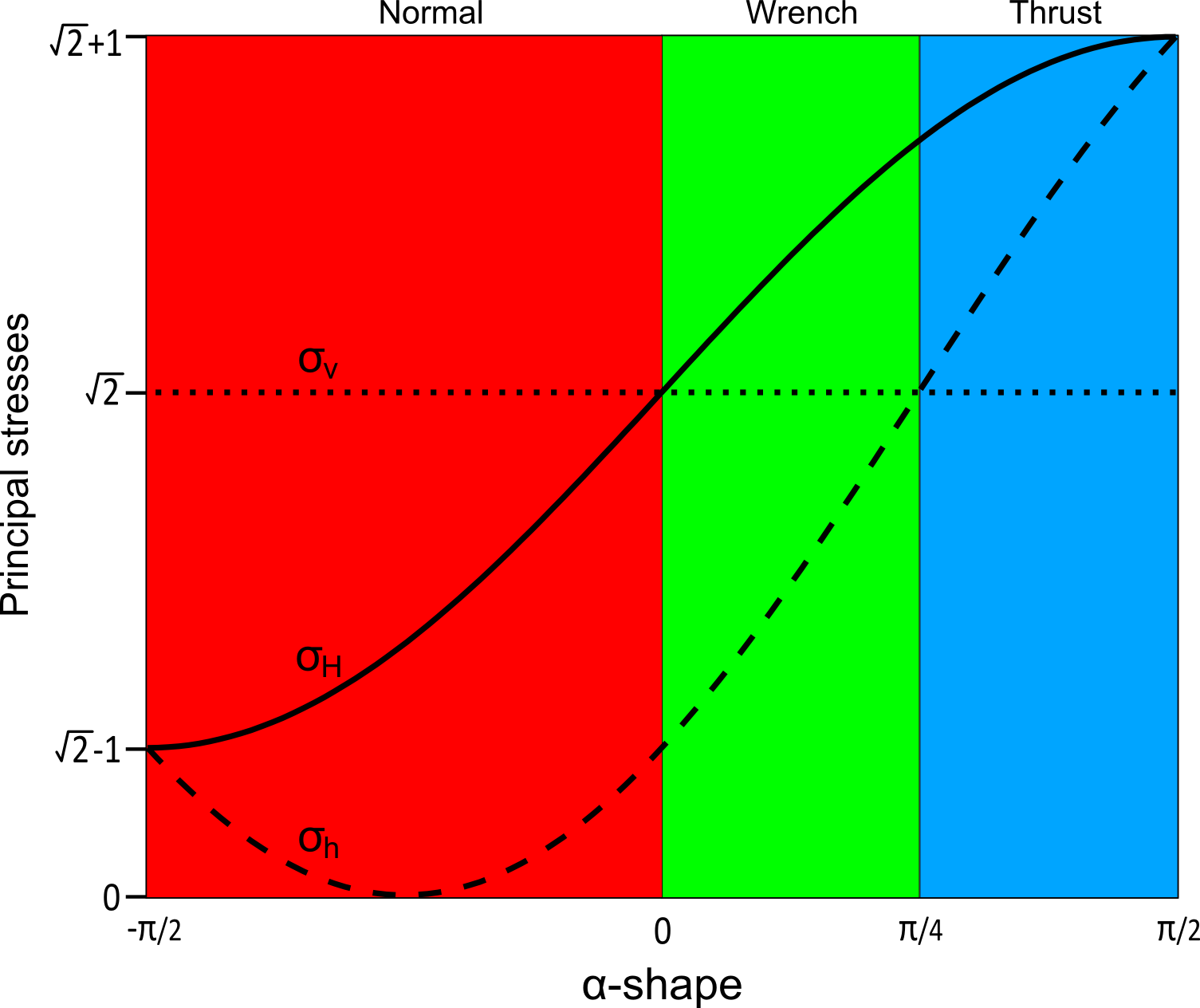
An Andersonian remote stress is a particular remote stress where one principal axis is vertical. Depending on the magnitude of vertical stress compared to the other two axis (maximum, minimum, intermediate), we have a different stress regimes.

All values are given in engineer convention, meaning that compression is negatif.

If the vertical axis corresponds to

  • the maximum principal stress: the regime is normal
  • the intermediate principal stress: the regime is strike-slip
  • the minimum principal stress: the regime is reverse
Anderson's faulting theory and stress regimes: a) strike-slip fault movement, when SH > SV > Sh; b) reverse or thrust fault movement, when SH > Sh > SV; and c) normal fault movement, when SV > SH > Sh.
example
const rho   = 2200 // Density of the rock
const Rh    = 0.1  // Normalized Sh according to Sv
const RH    = 0.6  // Normalized SH according to Sv
const g     = 9.81

const r = new arch.AndersoninanRemote()
r.setSh( (x,y,z) => Rh*rho*g*z )
r.setSH( (x,y,z) => RH*rho*g*z )
r.setSv( (x,y,z) => rho*g*z )
r.setTheta(35) // in degrees

console.log( r.valueAt([0, 0, -1000]) )

model.addRemote(r)

Hierarchy

  • AndersonianRemote

Implements

Index

Constructors

Methods

Constructors

constructor

Methods

R

  • R(): number
  • brief

    Get the stress ratio in [0, 1], which is (S2-S3)/(S1-S3) with S1 the maximum principal stress (compression is positive), S2 the intermediate and S3 the minimum principal stress. In addition, you have to call regime to know the the stress regime as there's an ambiguity to use only R to characterize an Andersoninan stress.

    see

    Rb

    Returns number

Rb

  • Rb(): number

alpha

  • alpha(): number
  • brief

    Another representation of the stress ratio and stress regime together using only one parameter which is an angle between -90° and +90°. This parameter is usually called alpha-shape. An explanation will be given soon to justify this representation.

    • for alpha in [-90° , 0°], we have a normal regime
    • for alpha in [ 0° , 45°], we have a strike-slip regime
    • for alpha in [45° , 90°], we have a reverse regime
    Representation of the alpha-shape as an angle
    Relations between alpha-shape and the three principale stresses

    Returns number

regime

  • regime(): string
  • brief

    Get the stress regime. Can be either normal, strike-slip or reverse

    Returns string

setSH

  • setSH(cb: number | Function): any
  • brief

    The magnitude of the maximum horizontal stress (Sigma H) which can be given by a number or a callback.

    default

    0

    Parameters

    • cb: number | Function

    Returns any

setSh

  • setSh(cb: number | Function): any
  • brief

    The magnitude of the minimum horizontal stress (Sigma h) which can be given by a number or a callback.

    default

    0

    Parameters

    • cb: number | Function

    Returns any

setSv

  • setSv(cb: number | Function): any
  • brief

    The magnitude of the vertical stress (Sigma v) which can be given by a number or a callback.

    default

    0

    Parameters

    • cb: number | Function

    Returns any

setTheta

  • setTheta(theta: number): any
  • brief

    The orientation in degrees of the maximum horizontal stress according to the North (global y-axis) and clock-wise.

    default

    0

    Parameters

    • theta: number

    Returns any

tractionAt

  • brief

    Evaluate the traction at pos(x,y,z) with normal n(x,y,z)

    Parameters

    • pos: Vector

      The position in 3D (e.g., center of a triangle)

    • normal: Vector

      The normal at point pos

    Returns Vector

    The traction vector in the form [x, y, z]

tractionAtSurface

  • brief

    Get the resolved stress at a surface's triangles

    Parameters

    Returns FlatVectors

    A flat array of tractions, one for each triangle making the surface

valueAt

  • brief

    Evaluate the remote at pos(x,y,z)

    Parameters

    • pos: Vector

      The position in 3D

    Returns Tensor

    The remote at pos. The returned array is in the form [xx, xy, xz, yy, yz, zz]